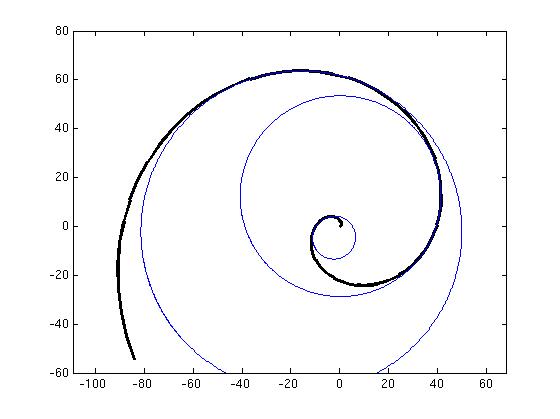
This diagram is of three nested circles of curvature on a (non cubic) spiral. Note that the spiral is always crossing into its circles of curvature as it is followed inward.
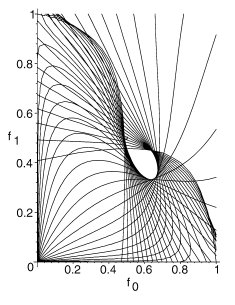
The black curves, found numerically, eliminate possible f0-f1 pairs which can yield cubic spirals. Remining white area indicates cubic spirals. The free variables f0-f1 are explained in the papers.
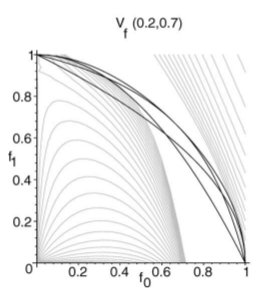
The gray curves, found numerically, eliminate possible f0-f1 pairs which can yield cubic spirals. Remining white area indicates cubic spirals. The black curves are for analytical purposes and are found algebraically. Tangents at ends are fixed.
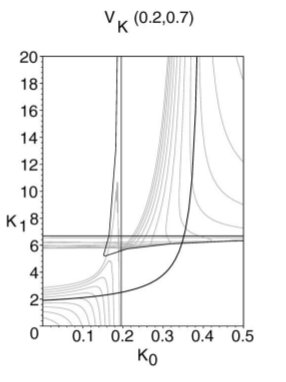
The gray and black curves in this diagram play exactly the same role as in the diagram to its left, except the two free variables are the curvatues at the endpoints of the cubic. The tangent angles at the endpoints are fixed (0.2 and 0.7).
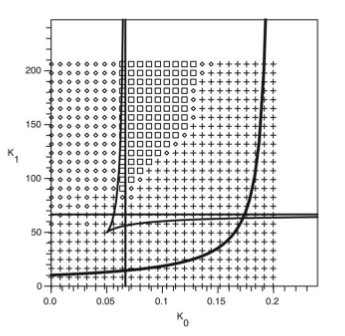
In this diagram, rational cubics are numerically analysed for fixed tangential conditions. Squares represent curvature constraints which may be satisfied by cubics alone. Diamonds indicate additional curvature combinations gained by allowing rational cubics rather than just cubics. The curve which begins roughly at (0,10) in the diagram represents the the boundary beyond which no spiral may occur due to simple geometric constraints.