This is an overview of some of the work I would like to pursue with undergraduates
There are several still-open questions involving the Towers of
Hanoi puzzle. The valid positions of a Towers of Hanoi puzzle can be
placed in a graph which turns out to be a Sierpinski triangle! Graph
adjacencies represent states having a distance of one move. It is
surprisingly simple (and fast) to compute the distance between any two
valid positions of a Towers of Hanoi. However, this calculation
involves computing two possible scenarios. Either the largest disc is
moved exactly once (this is the most common arrangment), or the
largest disc is moved twice. Additonal progress on this open problem
was made by Dan Romik in roughly 2003.
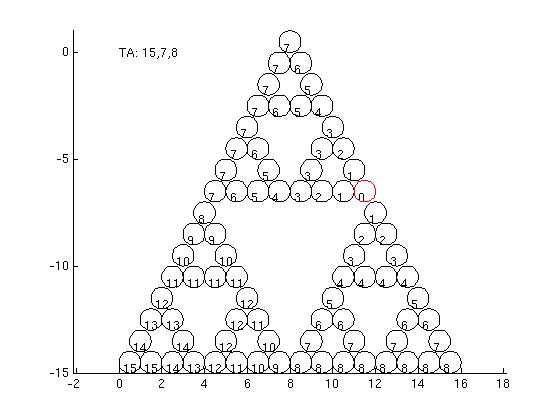
Distances from a given location within a Sierpinski triangle.
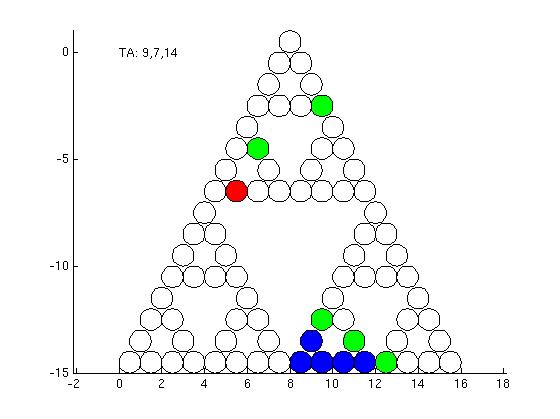
Green points have two minimal paths to the red point. Blue points have the property that the minimal path to the red point requires moving the largest disc twice in the corresponding Hanoi problem.
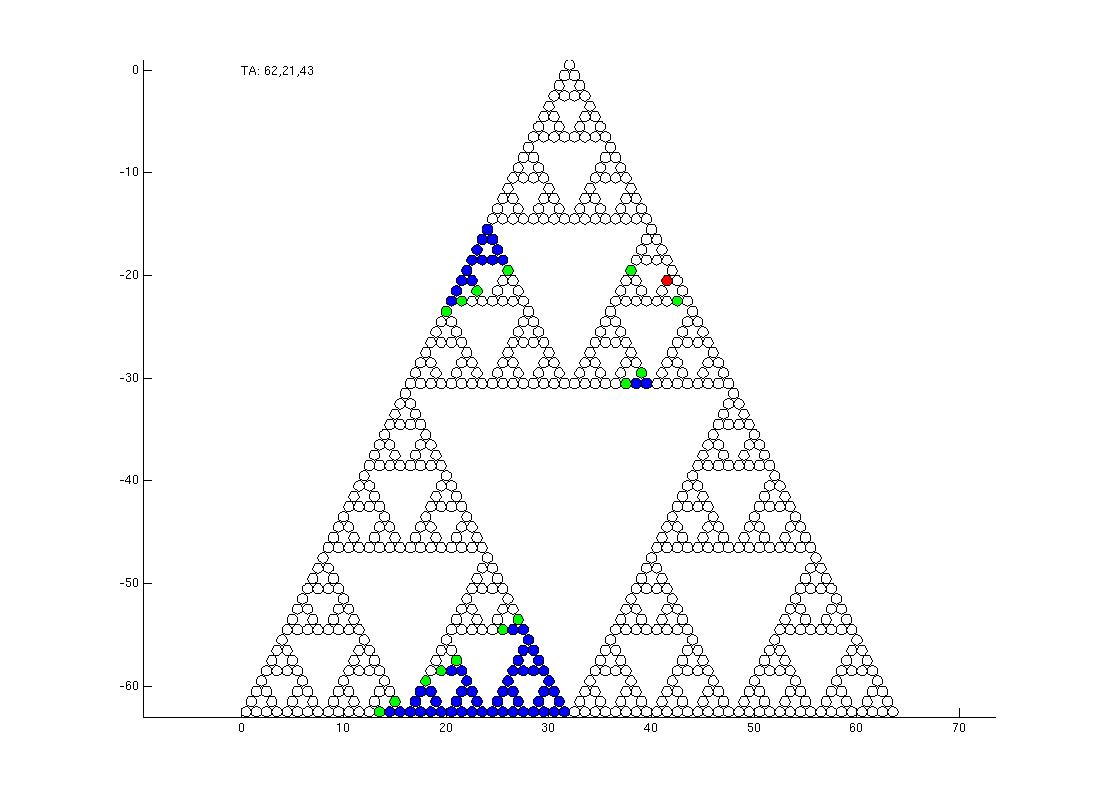
This is similar, but for a Hanoi puzzle with more discs. Points are colored blue if the largest disc which was moved at all moved twice.


