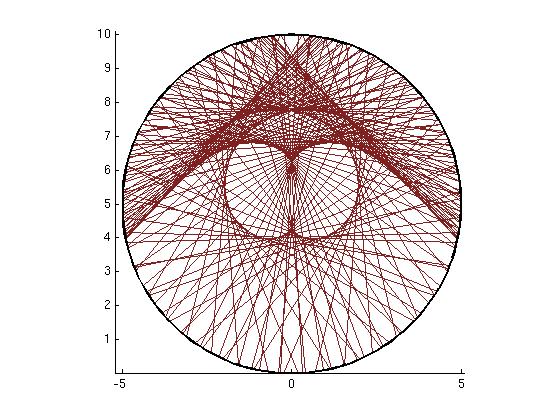
This is an overview of some of the work I've done in Ray Launching and Ray Tracing

Since arriving at Penn, I've been working on ray-launching problems which are tangentially related to work my husband/colleague is doing in topological imaging. I have been creating geometric simulations of wavefronts in MATLAB with the ultimate goal of making some geometric or topological hypotheses based on what is observed in the geometric simulations. This has been quite interesting and has opened up more questions than it has resolved.

This diagram shows the third level bounces of rays in a circle. The original point of the rays' origin was off-center. Note the lovely heart-shaped caustics!

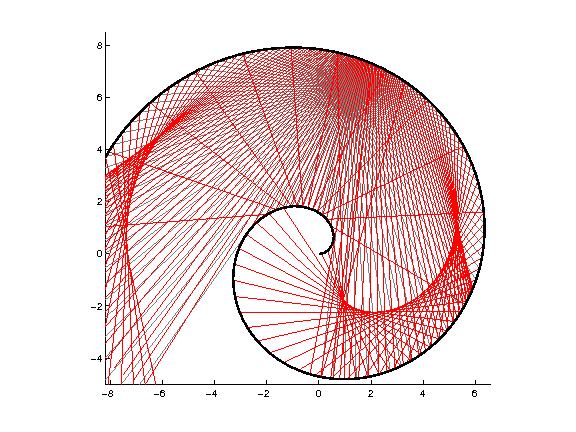
This diagram shows the original set of rays emanating from the source (gray) and the first set of bounced rays. The source is roughly at (2,6) in the diagram. Several characteristic trends are seen. The ever-present caustics are visible, as is the well-hidden center of the spiral. There is a region centered near (3,0), where the bounced rays are nearly parallel, indicating that rays bounced off a region nearly parabaloic in naure.

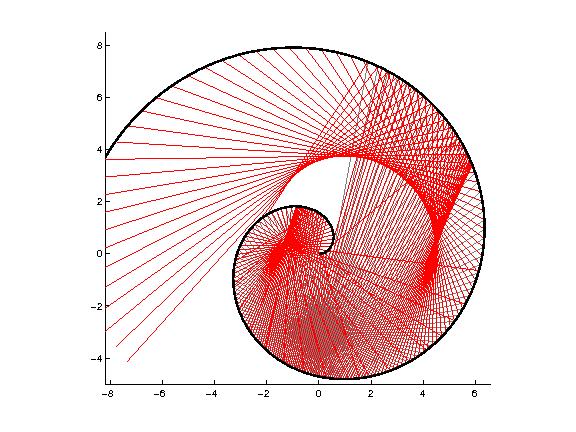
This diagram is the same as the one above, except that the source has moved to a location near (0,-3). The center of the spiral can now "hear" rays sooner.

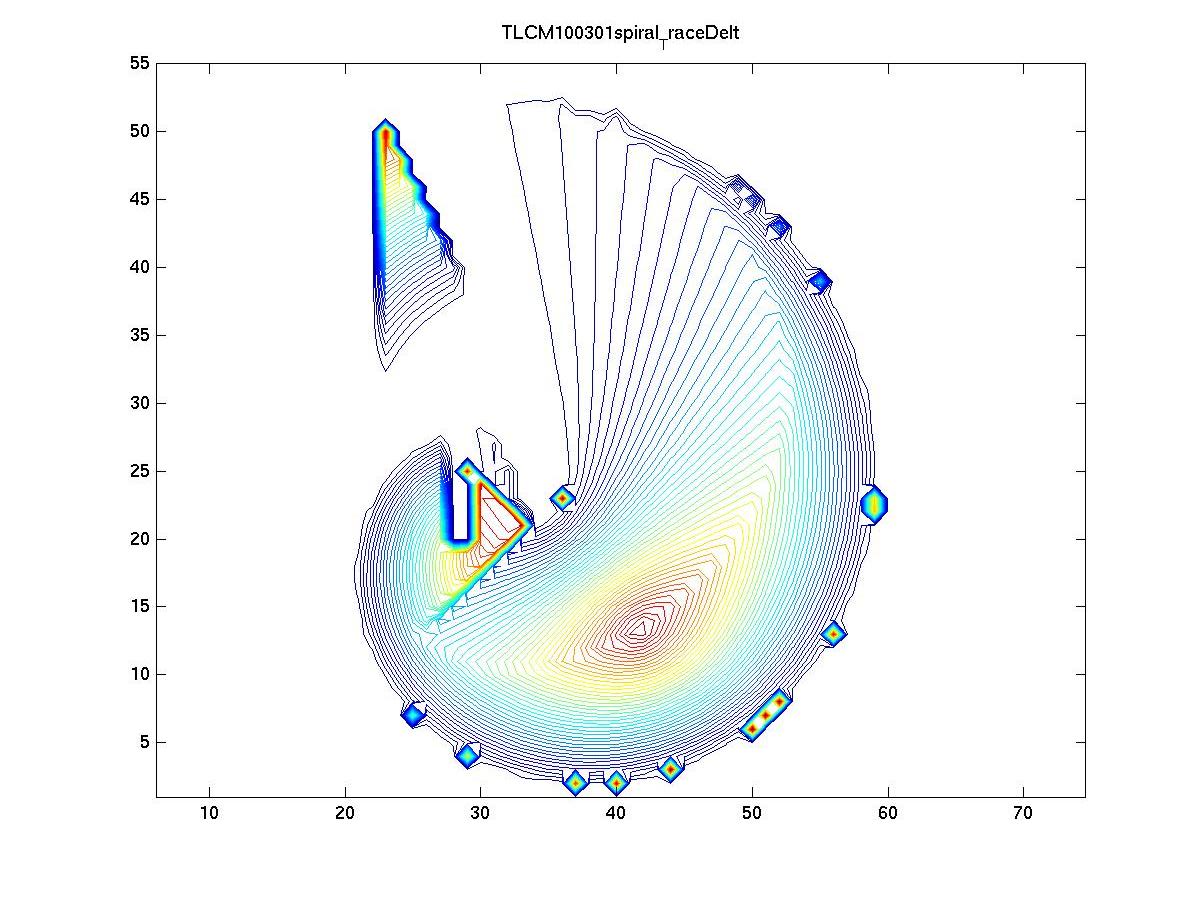
This diagram shows level curves in the time-difference-of-arrival domain (TDOA). This diagram was created using ray-tracing rather than ray-launching, so it is more accurate. However, ray-launching becomes computationally difficult after the first set of bounces, so I use ray-tracing to simulate bounces beyond the first.

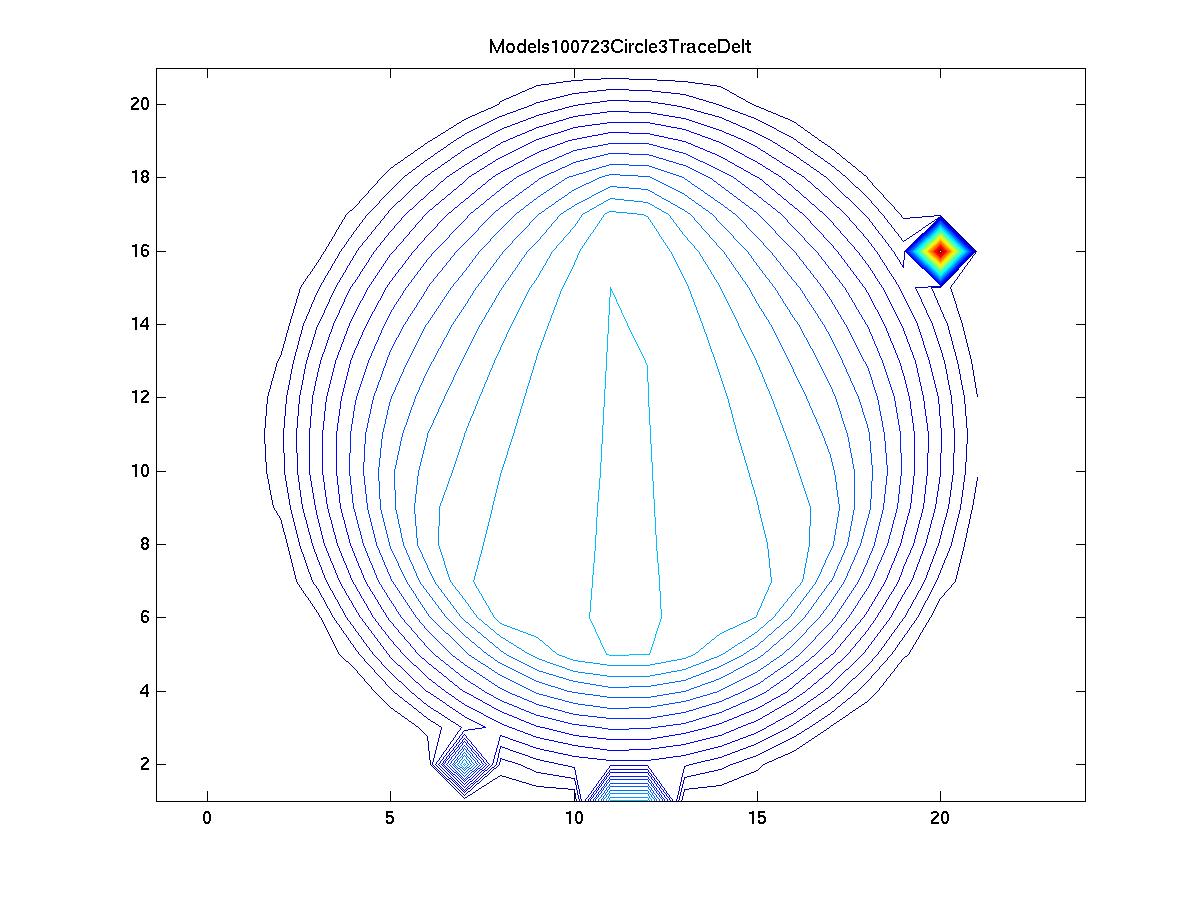
Ray-tracing is used again to detect level curves in the TDOA domain. Numerical issues are wildly obvious. However, most of the level curves are fairly smooth, which is what we expect. The level curves near boundaries have small TDOAs while the curves near the middles have larger TDOAs. The hope is to harness this trend to estimate the distance of a sensor to a wall. However, in more complex geometries, the issues compound rapidly.

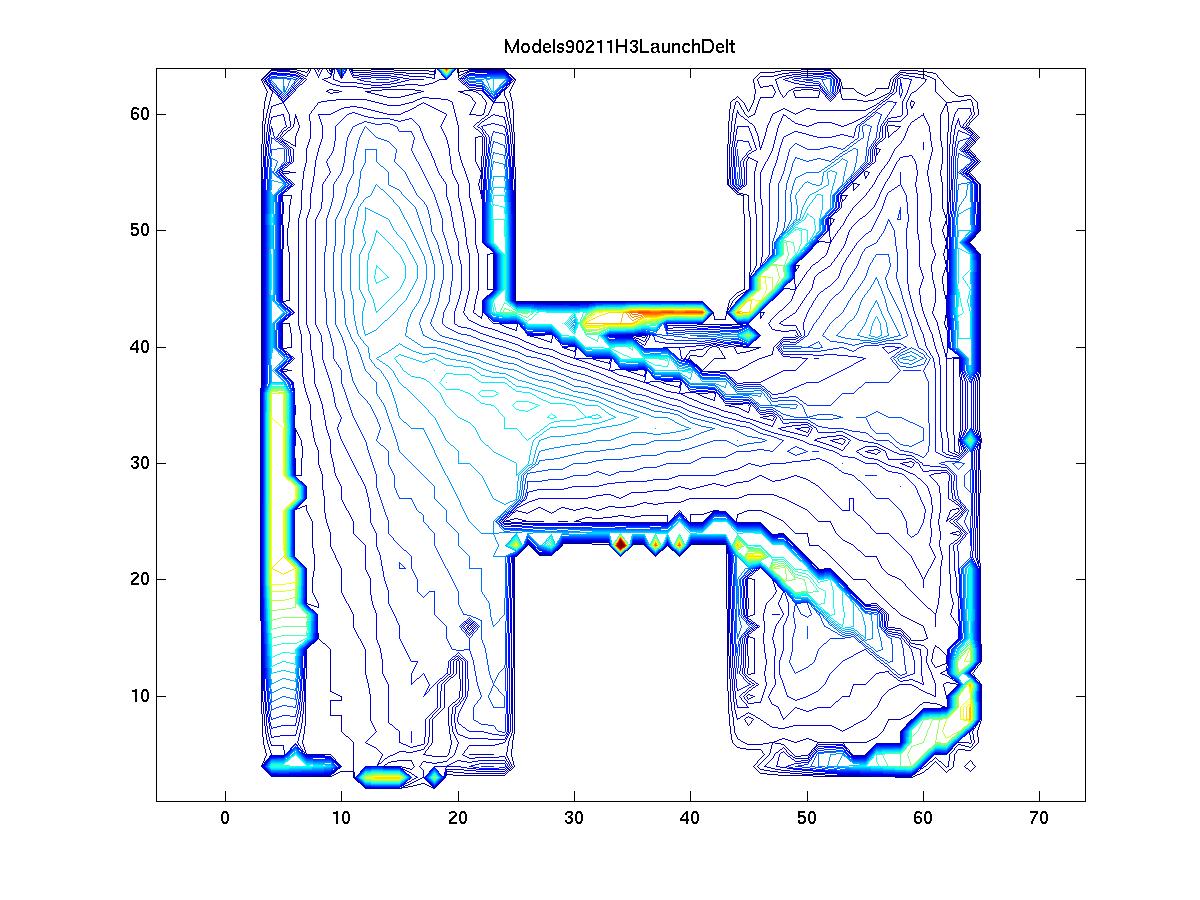
In this classical H-shaped geometry, ray-launching is used, because many areas of the geometry (which can be thought of as being in naturally occurring "cells") do not hear the first or even second bounce of the rays. Numerics are again quite obvious.

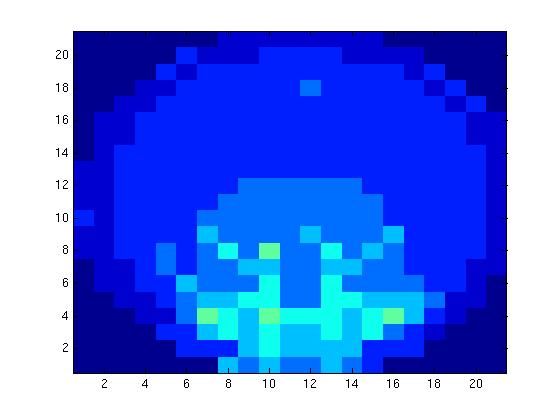
This diagram, which is one frame from an animation, shows which sensors have heard the signal a given number of times. The geometry is a simple circle with an off-center source.

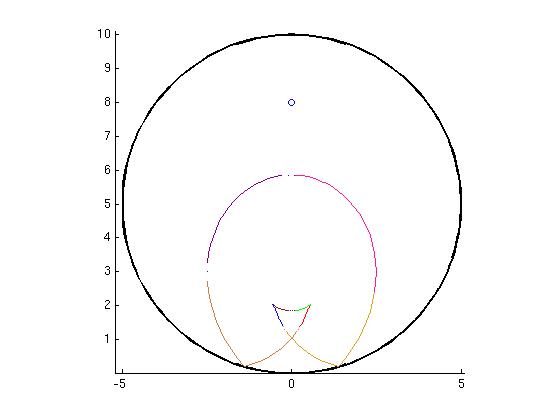
This is a frame from an animation which depicts a single wavefront emanating from a non-central point in a circle.